Capitolo 3 - La Terra
3.1 La Forma della Terra.
Se la Terra fosse perfettamente omogenea e immobile, la sua forma sarebbe quella di una sfera perfetta. In realtà essa non è omogenea ed è dotata di un moto di rotazione intorno al suo asse.
La forza centrifuga che deriva da questo movimento ha prodotto una deformazione che si manifesta con uno schiacciamento ai poli ed un rigonfiamento nelle zone equatoriali.
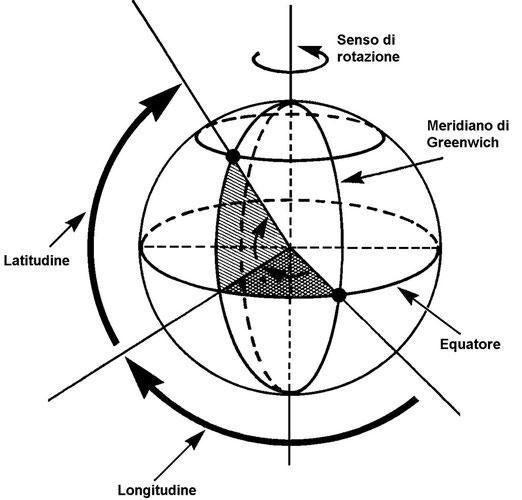
La forma che ne risulta (Figura 3.1), è simile a quella di un Ellissoide di rotazione, cioè quella che si ottiene facendo ruotare un ellisse intorno al suo asse minore.
L'asse minore dell'Ellissoide terrestre è rappresentato dalla linea congiungente i due poli, l'asse maggiore è uguale al diametro dell'Equatore.
La forza centrifuga si va a comporre con la forza di gravità, modificandone la direzione e l'intensità.
Il valore della forza centrifuga che si esercita su un oggetto di massa m che si trova sulla superficie terrestre può essere ricavata per mezzo delle seguenti formule:
Fc = m w2 R cosf
oppure:
Fc = m V2 : R cosf
dove:
Fc = Forza centrifuga
m = massa dell'oggetto
w = Velocità angolare della Terra
R = raggio terrestre
V = Velocità periferica della Terra alla Latitudine dell'oggetto
f = Latitudine dell'oggetto
Rcosf = distanza del punto dall'asse terrestre
La forza risultante dalla composizione vettoriale della forza gravitazionale e della forza centrifuga sarà massima ai poli, minima all'Equatore, e la sua direzione non passerà per il centro della Terra tranne che per i punti che si trovano ai poli e all'Equatore.
Ai poli l'unica forza agente è quella di gravitazione, essendo nulla la forza centrifuga. La direzione della forza passa quindi per il centro della Terra.
All'Equatore la forza centrifuga ha stessa direzione ma verso contrario rispetto alla forza gravitazionale, e va quindi a sottrarsi a questa. La forza risultante sarà di valore inferiore rispetto alla sola forza gravitazionale; la direzione non subirà modificazioni e quindi passerà per il centro della Terra.
Come si può osservare dalla Figura 3.2, a latitudini intermedie è necessario comporre vettorialmente la forza di gravitazione e la forza centrifuga. Si ottiene una risultante avente intensità variabile in funzione della Latitudine, e direzione che passa per l'asse della Terra, ma per un punto situato al di sotto del piano equatoriale.
Occorre considerare inoltre che il raggio terrestre all'Equatore è maggiore di 21 Km rispetto a quello al polo, perciò la forza di gravitazione che la Terra esercita su di un oggetto all'Equatore è minore rispetto a quella esercitata sullo stesso oggetto ai poli.
Si ricorderà che, secondo la legge di Newton, la forza di gravità varia in modo inversamente proporzionale al quadrato delle distanze tra i baricentri degli oggetti considerati, e quindi gli oggetti all'Equatore essendo più lontani dal centro della Terra saranno sottoposti ad una forza attrattiva minore.
Abbiamo quindi ai poli una forza gravitazionale maggiore, e all'Equatore una forza gravitazionale minore, dalla quale va sottratta inoltre la forza centrifuga.
Il valore medio dell'accelerazione di gravità, valido con sufficiente approssimazione su tutta la Terra è di 9,81 m/sec2.
3.2 Il Geoide.
Un Ellissoide di rotazione riesce a fornire soltanto una approssimazione, sia pur buona, della forma che assumerebbe la Terra se il livello medio del mare si estendesse anche là dove si trovano le terre emerse, colmando le eventuali depressioni ed eliminando tutti i rilievi.
In effetti la Terra non è omogenea, e la presenza di materia di densità diversa provoca una leggera distorsione del campo gravitazionale, sia per quello che riguarda la direzione che l'intensità.
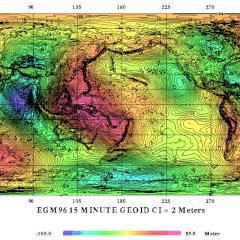
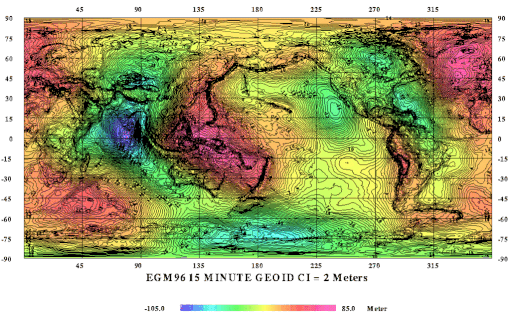
Il Geoide (parola che deriva dal greco geo, tratto da ge "Terra", e oeides, che significa "simile a"), è una superficie equipotenziale non esprimibile attraverso una formula matematica, costituita dall'insieme dei punti in cui la superficie è perpendicolare al filo a piombo.
La superficie del Geoide si discosta di pochi metri da quella dell'Ellissoide. In generale si nota che in corrispondenza di fosse oceaniche il Geoide si trova al di sotto dell'Ellissoide, e coincide con il livello medio del mare; in corrispondenza di catene montuose il Geoide si situa al di sopra dell'Ellissoide (Figure 3.3 e 3.4).
Ai fini pratici della Navigazione è sufficiente considerare la Terra sferica, in quanto l'errore commesso è talmente piccolo da poter essere trascurato.
3.3 La forza deviante di Coriolis.
Ogni punto della Terra compie in un giorno un giro intero di 360 gradi intorno all'asse, qualunque sia la lunghezza del Parallelo da esso descritto; la Velocità lineare, ossia la distanza percorsa da un Punto nell'unità di Tempo varia perciò con la Latitudine (Figura 3.5).
Un punto sull’equatore percorre l’intera circonferenza pari a 40.000 Km nelle 24 ore, mentre uno situato al polo rimane fermo.
Si va da un massimo di velocità pari a circa 463 metri al secondo all'Equatore (1668 Km/h) fino ad un valore minimo di 0 ai poli.

La diversa velocità lineare dei punti della Terra che si trovano a differenti latitudini ha notevoli conseguenze per ciò che riguarda il moto dei corpi sulla sua superficie. Questi infatti sono sottoposti all'azione di una forza apparente deviante (detta forza di Coriolis), proporzionale alla velocità di movimento e al seno della Latitudine.
Fd = 2 m V w senf
dove:
Fd = forza deviante di Coriolis
m = massa dell'oggetto
V = Velocità dell'oggetto
w = Velocità angolare di rotazione della Terra
f = Latitudine dell'oggetto
L'effetto della forza di Coriolis è quello di deviare verso destra il moto degli oggetti nell'emisfero boreale, e verso sinistra quello degli oggetti nell'emisfero australe (Figura 3.6).
Inoltre dalla relazione si desume che per un corpo che si muove sulla superficie terrestre la forza deviante è direttamente proporzionale al seno della Latitudine, ed è quindi massima ai poli e nulla all'Equatore.
Più correttamente, volendo considerare il moto in una qualsiasi direzione (per esempio verticale), occorre passare dalle grandezze scalari ai vettori rappresentativi delle stesse, prendendo in considerazione anche il verso oltre che il modulo.
Fd = 2 m w L V
Le lettere sottolineate indicano i vettori delle grandezze corrispondenti.
Il simbolo L indica il prodotto vettoriale.
3.4 Le dimensioni della Terra.
I primi tentativi per determinare le dimensioni del nostro pianeta di cui ci siano giunte notizie risalgono al IV secolo A.C.
Nel III secolo A.C. Eratostene di Cirene, usando un sistema abbastanza semplice ed ingegnoso ottenne risultati notevolmente buoni.
Egli riteneva che le città di Alessandria d'Egitto e di Siene, l'attuale Assuan fossero situate sullo stesso Meridiano, (cosa non perfettamente esatta), e conosceva la loro distanza, che valutava in 5.000 stadi egizi.
Eratostene aveva osservato che a Siene, il giorno del solstizio d'estate, a mezzogiorno il Sole si specchiava sul fondo dei pozzi, i corpi non facevano ombra: questo voleva dire che il Sole era perfettamente allo Zenit. Egli misurò quindi l'angolo che facevano i raggi del Sole con la verticale lo stesso giorno ad Alessandria d'Egitto (Figura 3.7).
Quest'angolo risultò essere pari alla cinquantesima parte della intera circonferenza.
Considerando uguale l'angolo al centro della Terra tra Siene e Alessandria e l'angolo tra i raggi solari e la verticale di Alessandria, mediante una semplice proporzione, Eratostene riuscì a valutare la circonferenza meridiana della Terra in 50x5.000 stadi, ovvero 250.000 stadi egiziani, equivalenti ad una misura di 39.375 Km, valore sorprendentemente vicino a quello oggi accettato che è di 40.009 Km.
Le dimensioni della Terra costituiscono la base del sistema metrico decimale, fissato nel 1793 dall'Accademia delle Scienze di Parigi. Questa, dopo aver fatto eseguire accurate misure in varie parti del globo, stabiliva la nuova unità di misura: il metro, definendolo come la quarantamilionesima parte del Meridiano terrestre, e faceva costruire un campione di lunghezza corrispondente, composto da una lega di platino e iridio, che viene tuttora conservato nell'Archivio Nazionale di Pesi e Misure di Parigi.
In seguito si constatò che il Meridiano terrestre è un po' più lungo di 40 milioni di metri, e per l'esattezza 40.009.152 m; il campione suddetto, per rappresentare esattamente la quarantamilionesima parte del Meridiano dovrebbe essere allungato di circa 2 decimi di millimetro.
Attualmente un campione di questo genere non offre più la precisione richiesta dalla tecnica moderna; perciò in campo internazionale il metro viene oggi definito come multiplo di una particolare lunghezza d'onda della luce emessa dal Krypton 86.
Le più recenti misure astro-geodetiche condotte per mezzo di satelliti in orbita intorno alla Terra hanno permesso di stabilire la lunghezza del raggio equatoriale in 6378,16 Km e quella del raggio polare in 6356,16 Km, con una differenza di 21,38 Km e uno schiacciamento polare pari a 1/298,3.
L'Unione Geodetica Internazionale ha deciso di assumere come solido di riferimento, a rappresentazione della forma della Terra, l'Ellissoide di rotazione.
Le dimensioni della Terra secondo l'Ellissoide internazionale sono riportate nella tabella seguente:
|
Raggio max. equatoriale |
m |
6.378.388 |
|
Raggio min. polare |
m |
6.356.912 |
|
Schiacciamento polare |
|
1/297 |
|
Raggio di una sfera avente lo stesso volume della Terra |
m |
6.371.221 |
|
Raggio di una sfera avente la stessa superficie della Terra |
m |
6.371.228 |
|
Lunghezza del circolo Meridiano |
m |
40.009.152 |
|
Lunghezza dell'Equatore |
m |
40.076.594 |
|
Superficie totale della Terra |
Km2 |
510.100.000 |
|
Superficie delle terre emerse |
Km2 |
149.400.000 |
|
Superficie degli oceani |
Km2 |
360.700.000 |
|
Massa della Terra |
g |
5,976 x 1027 |
|
Volume della Terra |
Km3 |
1.083.319.780.000 |
|
Densità media della Terra |
g/cm3 |
5,52 |
|
Accelerazione di gravità sulla superficie della Terra (valore medio) |
m/s2 |
9,81 |
Ai fini della Navigazione è sufficiente considerare la Terra sferica, con un raggio di 6371 Km.
Alcuni valori legati alle dimensioni terrestri sono di particolare utilità per le applicazioni pratiche, come ad esempio il miglio marino che è definito come la lunghezza media di un primo di Meridiano.
Ricordando che l'angolo corrispondente all'arco di Meridiano compreso tra Equatore e polo è di 90°, che ogni grado è divisibile in 60 primi (5400 primi in 90°), che la distanza tra l'Equatore ed il polo è di circa 10.000 Km, abbiamo per il primo di Meridiano la lunghezza di:
10.000 : 5.400 = 1,852 Km / primo di Meridiano
3.5 Asse di rotazione e Poli geografici, Meridiani e Paralleli.
Sulla Terra, considerata sferica, è possibile tracciare alcune linee che risultano di notevole utilità: l'insieme di queste linee infatti costituisce un sistema di riferimento idoneo a localizzare gli oggetti che si trovano sulla sua superficie.
Prendiamo Innanzitutto in considerazione l'asse terrestre, che passa per il centro della Terra e definisce sulla sua superficie la Posizione dei poli Nord e Sud.
Immaginiamo poi un piano perpendicolare all'asse e passante per il centro della Terra: tale piano dividerà la sfera in due emisferi: quello settentrionale o boreale dalla parte del Polo Nord, e quello meridionale o australe dalla parte del Polo Sud.
Esso determinerà inoltre sulla superficie sferica una circonferenza massima equidistante dai poli chiamata Equatore.
L'intersezione tra la superficie terrestre e i piani perpendicolari all'asse ma non passanti per il centro della Terra, sarà rappresentata da cerchi minori detti Paralleli; questi saranno di lunghezza massima all'Equatore e via via decrescente procedendo verso i poli (Figura 3.8).
Immaginiamo ora di tagliare la sfera terrestre con dei piani contenenti l'asse, e quindi perpendicolari al piano equatoriale. Avremo tanti circoli massimi, tutti uguali tra loro e passanti per i poli, chiamati Meridiani (Figura 3.9).


Comunemente si considerano come Meridiani le semicirconferenze comprese tra un polo e l'altro, avendo ognuno di essi il proprio antimeridiano nella semicirconferenza opposta.
Essendo delle linee immaginarie, i Paralleli e i Meridiani sono in numero infinito. Considerando però quelli tracciati a distanza di un grado l'uno dall'altro, possiamo dire che i Meridiani sono 360 (valutando le semicirconferenze), e i Paralleli sono 179: l'Equatore, 89 Paralleli a nord e 89 a sud di questo. Il novantesimo Parallelo nord e sud, coincidendo con i poli si riducono ad un punto.
In realtà possiamo immaginare tanti Paralleli e tanti Meridiani quanti ne vogliamo, onde farne passare uno per qualsiasi punto della superficie terrestre.
La rete formata dai Meridiani e dai Paralleli rappresenta il reticolato geografico.
Le sue maglie sono costituite da trapezi sferici, ad eccezione di quelle aventi vertice nei poli, che hanno la forma di triangoli sferici.
Il reticolato geografico consente di determinare la Posizione di un Punto sulla superficie terrestre allo stesso modo con cui un sistema di coordinate cartesiane permette di individuare la Posizione di un Punto su un piano (Figura 3.10).
3.6 Latitudine e Longitudine.
Definiamo a questo punto le coordinate geografiche, che sono la Latitudine e la Longitudine (Figura 3.11).
La Latitudine è la distanza angolare di un punto dall'Equatore; può essere Nord o Sud a seconda che il punto si trovi nell'emisfero boreale o in quello australe; essa corrisponde all'ampiezza dell'angolo avente il vertice nel centro della Terra che sottende l'arco di Meridiano compreso tra il punto considerato e l'Equatore.
Tutti i punti che si trovano sull'Equatore hanno Latitudine 0°. Il valore massimo di Latitudine è di 90° Nord o 90° Sud per punti che si trovano ai poli.
La Longitudine è la distanza angolare di un punto dal Meridiano di Greenwich, misurata sull'arco di Parallelo che passa per quel punto; può essere Est o Ovest a seconda che il punto si trovi ad oriente o ad occidente del Meridiano di riferimento; essa corrisponde all'ampiezza dell'angolo avente il vertice nel centro della Terra che sottende un arco di Equatore compreso tra il Meridiano di Greenwich e il Meridiano passante per il punto.
Tutti i punti situati sul Meridiano di Greenwich hanno Longitudine 0°. I punti situati sul suo antimeridiano hanno Longitudine 180°.
I cerchi massimi assunti come riferimento sono quindi l'Equatore e il Meridiano che passa per l'osservatorio astronomico di Greenwich (Londra).
Ad ogni coppia di valori di Latitudine e Longitudine corrisponde un Punto sulla Terra; viceversa ogni Punto sulla Terra è identificabile univocamente per mezzo di una coppia di valori: Latitudine e Longitudine (Figura 3.12).
Possiamo dire quindi che esiste una corrispondenza biunivoca tra l'insieme dei valori possibili di Latitudine e Longitudine e l'insieme dei punti della superficie terrestre.
3.7 Cerchi massimi.
Si definisce cerchio massimo quello ottenuto dall'intersezione della sfera terrestre con un piano passante per il suo centro. Tale piano divide la sfera in due emisferi uguali; casi particolari di cerchio massimo sono l'Equatore e i Meridiani.
L'importanza di questo genere di curva deriva dal fatto che la distanza minima tra due punti sulla superficie terrestre corrisponde all'arco di cerchio massimo minore di 180° che li unisce (Figura 3.13).
Ogni piano non passante per il centro della Terra, intersecando la superficie terrestre genera un cerchio minore. I Paralleli sono cerchi minori.
3.8 Uso delle coordinate Latitudine e Longitudine.
Il primo uso delle coordinate geografiche, è quello di individuare un punto sulla Carta geografica conoscendone le coordinate, e viceversa ricavare le coordinate di un punto indicato sulla Carta.
Qualora il punto non cada esattamente sui Meridiani e sui Paralleli tracciati occorre effettuare un'interpolazione tra quelli tracciati più vicini.
E' possibile effettuare calcoli di differenza di Latitudine e Longitudine sia graficamente, direttamente sulla Carta, sia analiticamente, mediante semplici operazioni algebriche.
Il valore massimo di differenza di Latitudine è di 180°, nel caso di due punti situati uno al Polo Nord e uno al Polo Sud. In tutti gli altri casi è sempre minore di 180°.
Anche la massima differenza di Longitudine è di 180°, e questa corrisponde a qualsiasi coppia di punti situati uno sull'antimeridiano dell'altro.
Dovendo calcolare la differenza di Latitudine tra due punti, se questi si trovano nello stesso emisfero, occorrerà fare la differenza dei valori delle loro coordinate (Figura 3.14).
La differenza di Latitudine tra due punti che si trovano in emisferi opposti sarà data dalla somma dei valori delle coordinate (Figura 3.15).
Se si assume convenzionalmente per le latitudini Nord il segno + e per le latitudini Sud il segno - la differenza di Latitudine può essere calcolata con una semplice differenza algebrica.
Df = fB - fA
fN = +
fS = -
Il risultato è positivo se il Punto B si trova a Nord del Punto A. E' negativo in caso contrario.
Per calcolare la differenza di Longitudine tra due punti, se questi hanno entrambi Longitudine dello stesso nome (Est o Ovest), occorrerà fare la differenza dei valori delle loro coordinate (Figura 3.16).
Per i calcoli di differenza di Longitudine tra punti aventi uno Longitudine Est e un altro Longitudine Ovest, occorrerà fare la somma dei valori delle coordinate (Figura 3.17). Qualora il risultato ottenuto sia superiore a 180°, il valore corretto di differenza di Longitudine sarà calcolato sottraendo da 360° il risultato precedentemente ottenuto (Figura 3.18).
Qualora il risultato ottenuto sia superiore a 180°, il valore corretto di differenza di longitudine sarà calcolato sottraendo da 360° il risultato precedentemente ottenuto (Figura 3.18)
Se si assume convenzionalmente per le longitudini Est il segno + e per le longitudini Ovest il segno - la differenza di Longitudine può essere calcolata come una semplice differenza algebrica.
Dl = lB - lA
lE = +
lW = -
Se il risultato è positivo il Punto B si trova ad Est del Punto A.
E' ad Ovest in caso contrario.
Qualora il risultato ottenuto sia maggiore di 180°, si ricava il valore corretto di differenza di Longitudine sottraendo da 360° il valore trovato: (360° - Dl).

3.9 Ortodromia.
L'Ortodromia (dal greco orthodromeo, che vuol dire "correre dritto"), è l'arco di cerchio massimo minore di 180° che unisce due punti sulla sfera terrestre. Questa è la distanza minima tra i due punti. I Meridiani vengono tagliati dalla curva ortodromica con angoli variabili lungo tutta la sua lunghezza (Figura 3.19).
Per determinare la lunghezza di un percorso ortodromico occorre applicare alcune formule di trigonometria sferica, capaci di risolvere un triangolo sferico.
Questo, al pari di un qualsiasi triangolo, è caratterizzato dai suoi lati, dai suoi vertici e dai suoi angoli.
Le differenze principali consistono nel fatto che i lati, anziché essere rettilinei, sono archi di circonferenza, e che la somma degli angoli interni non è più costante e uguale a 180°, ma può variare da un minimo di 180° ad un massimo di 540°.
Il comune triangolo piano, non è che un caso particolare di triangolo sferico, e le formule trigonometriche che legano gli elementi del triangolo piano, non sono che le formule del triangolo sferico semplificate (se dalla sfera si passa all’ellissoide di rotazione, le formule si complicano ulteriormente).
Nel triangolo sferico i vertici sono:
- il polo
- il punto A
- il punto B
I lati sono:
- l’arco di meridiano che congiunge il punto A con il polo, identificato dalla lettera “b”
- l’arco di meridiano che congiunge il punto B con il polo, identificato dalla lettera “a”
- la curva ortodromica tra A e B, identificata dalla lettera “c”
Gli angoli sono:
- l’angolo formato tra l'Ortodromia e il Meridiano passante per il punto A, identificato dalla lettera “A^”
- l’angolo formato tra l'Ortodromia e il Meridiano passante per il punto B, identificato dalla lettera “B^”
- la differenza di Longitudine fra i punti A e B, identificata dalla lettera “C^”
(Figura 3.20).
La formula di Eulero che fornisce il coseno dell'arco ortodromico è la seguente:
cos c = cos a cos b + sen a sen b cos C^
In questa relazione con le lettere minuscole sono indicati i lati, e con le lettere maiuscole gli angoli opposti corrispondenti.
Conoscendo la misure dei due lati e il valore dell'angolo compreso è possibile quindi calcolare la misura del terzo lato incognito.
Nella figura, ai lati vanno attribuiti i valori seguenti:
a = distanza polare del Punto B = 90 - fB
b = distanza polare del Punto A = 90 - fA
c = lunghezza del percorso ortodromico
A^ = angolo tra Meridiano e percorso ortodromico nel punto A
B^ = angolo tra Meridiano e percorso ortodromico nel punto B
C^ = differenza di Longitudine tra A e B = fB - fA
Occorre poi calcolare l'arco coseno, che deve essere infine trasformato da gradi in primi, corrispondenti a miglia nautiche, ottenendo così la lunghezza del percorso ortodromico cercato.
Fino all'avvento dei calcolatori tascabili era pressoché impossibile utilizzare direttamente queste formule ricavate dalla trigonometria sferica, e i matematici avevano ideato una serie di metodi per semplificare i calcoli, che prevedevano comunque l'uso di tavole trigonometriche per la risoluzione del triangolo sferico. Attualmente, potendo utilizzare computer e calcolatrici programmabili, può essere utile e più veloce conoscere le relazioni fondamentali che legano gli elementi del triangolo sferico, al fine di calcolare gli elementi ignoti, avendo gli altri dati a disposizione.
Mantenendo la simbologia sopra indicata riportiamo ora la relazione tra i lati e gli angoli opposti, o teorema dei seni:
sen a / sen A^ = sen b / sen B^ = sen c / sen C^
Un'altra relazione interessante è quella delle cotangenti, o relazione tra quattro elementi consecutivi:
cotg a sen b = cos b cos C^ + sen C^ cotg A^
Le relazioni sopra riportate hanno validità generale per quanto riguarda la risoluzione di triangoli sferici.
Esempio.
Calcolare la distanza ortodromica tra gli aeroporti di Mosca e Milano.
Coordinate di Mosca: N55°58'00"; E037°25'00" = Punto A
Coordinate di Milano: N45°26'30"; E009°16'42" = Punto B
La formula da applicare è quella di Eulero:
cos c = cos a cos b + sen a sen b cos C^
a = dist. polare del Punto B = 90° - fB
a = 90°00'00" - 45°26'30" = 44°33'30"
b = dist. polare del Punto A = 90° - fA
b = 90°00'00" - 55°58'00" = 34°02'00"
C^ = diff. di long. tra A e B = fB - fA
C^ = 037°25'00" - 009°16'42" = 28°08'18"
cos c = cos 44°33'30" * cos 34°02'00" + sen 44°33'30" * sen 34°02'00" * cos 28°08'18" = 0.93676
c = arc cos 0.93676 = 20°29'
trasformando l'arco in distanza si ha:
c = 20 * 60 + 29 = 1229 miglia nautiche
3.10 Lossodromia.
Vi è un'altra curva di interesse per le sue caratteristiche peculiari: è la Lossodromia (la parola deriva dal greco loksodromos che significa "che corre obliquamente").
Questa curva unisce due punti sulla superficie della Terra tagliando tutti i Meridiani con lo stesso angolo (Figura 3.21).
La Lossodromia ha una lunghezza che è sempre maggiore o uguale a quella della Ortodromia corrispondente.
La Lossodromia si avvolge a spirale intorno ai poli mantenendo sempre lo stesso angolo con i Meridiani. L'Equatore corrisponde ad un punto di flesso.
Per brevi percorsi e latitudini non troppo elevate la differenza tra Ortodromia e Lossodromia è minima; è quindi utilizzabile una curva lossodromica senza incorrere in errori apprezzabili al fine di sfruttare la sua caratteristica che è quella di mantenere un angolo costante con i Meridiani, rendendo quindi più facile la condotta della Navigazione (Figura 3.22).
Per lunghi percorsi l'Ortodromia può essere divisa in brevi tratti, tra i quali tracciare segmenti di Lossodromia: si ottiene una spezzata lossodromica che ha i pregi di entrambe le curve: distanza più breve tra i punti e facilità di condotta della Navigazione.
Equatore e Meridiani sono contemporaneamente ortodromie e lossodromie.
3.11 Brachistocrona.
Esaminiamo brevemente un'altra linea chiamata brachistocrona (dal greco brakhistos, superlativo di brakhys, che significa "corto" e khronos, che significa "Tempo"), o percorso di minor Tempo.
Questa viene calcolata in funzione dei venti effettivi in quota, e può discostarsi variamente dagli altri percorsi esaminati, al fine di utilizzare al meglio i venti favorevoli o di evitare le zone di forte vento contrario associate alle correnti a getto (Figura 3.23).
 NAVIGAZIONE AEREA
di:
Enrico Della Gatta
NAVIGAZIONE AEREA
di:
Enrico Della Gatta