Capitolo 9 - Carte per la Navigazione Aerea

9.1       Carta di Mercatore

Nella Navigazione aerea le Carte più usate sono le seguenti:

• Carta di Mercatore

• Carta di Lambert

• Carta stereografica della zona polare

• Carta gnomonica

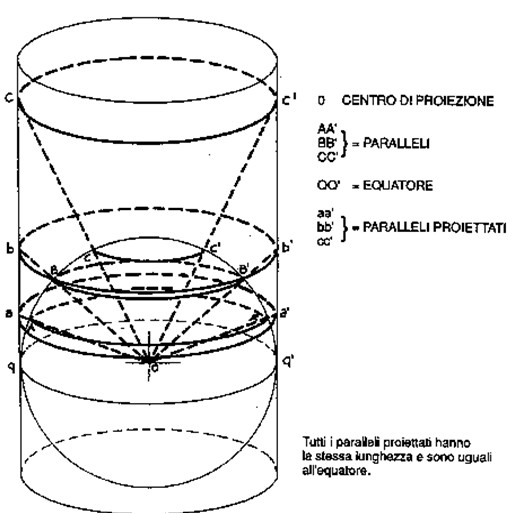
Come già accennato in precedenza, la Carta di Mercatore è derivata dalla proiezione per sviluppo cilindrica retta, che si ottiene proiettando su di un cilindro tangente all'Equatore il reticolo formato sulla sfera dai meridiani e dai paralleli, adottando il centro della Terra quale punto di vista.

Si immagina di avvolgere la sfera rappresentativa con una superficie cilindrica, facendo in modo che i punti di contatto (tangenza) siano quelli dell'Equatore. La lunghezza dell'Equatore sulla sfera rappresentativa verrà riprodotta sulla proiezione in grandezza vera e sarà questa la linea isomecoica della proiezione (dal greco isos "uguale" e mêkos "lunghezza"). Solo su tale linea risulterà valida la Scala. L'Equatore non subisce quindi alcuna alterazione.

Sulla sfera terrestre i meridiani giacciono su un piano che contiene anche l'asse di rotazione. Immaginando di proiettarli dal centro della Terra sul cilindro tangente, otterremo delle rette parallele all'asse terrestre, individuate dall'intersezione della superficie cilindrica con il piano di giacenza di ogni meridiano proiettato (Figura 9.1).

Potremo affermare che tutti i meridiani sono rappresentati da un fascio di rette parallele che costituiscono quindi la superficie del cilindro. Sulla Terra, la lunghezza effettiva dei meridiani tra i due poli è pari a R, dove con R indichiamo il raggio terrestre. Sulla proiezione, invece, trattandosi di cilindro indefinito, le generatrici hanno lunghezza infinita. A causa della proiezione vi è stata una deformazione dimensionale dei meridiani.

Vediamo ora la funzione con cui avviene la deformazione dimensionale dei meridiani. Prendiamo in esame il tratto di meridiano compreso tra l'Equatore ed uno dei poli. Sulla sfera questo arco ha una lunghezza ben definita (circa 10.000 Km) e rappresenta un arco di 90°. Sulla proiezione lo stesso tratto di meridiano è rappresentato da una semiretta indefinita con origine nel punto di tangenza. Su tale semiretta giacciono e si misurano le tangenti trigonometriche dell'arco che sulla sfera rappresenta il meridiano. Da ciò si deduce che la deformazione dimensionale dei meridiani avviene con la legge della tangente.

Per quanto riguarda i paralleli, la proiezione dal centro della Terra di questi sulla superficie cilindrica tangente corrisponde a cerchi ottenuti dalla intersezione di coni aventi vertice nel centro della Terra, passanti per ogni singolo parallelo e intersecanti poi il cilindro, a distanze dall'Equatore progressivamente crescenti con la Latitudine del parallelo proiettato (Figura 9.2).

La lunghezza in miglia nautiche di un tratto di Equatore sulla sfera terrestre è pari alla differenza di Longitudine espressa in primi. Ad una qualsiasi Latitudine , la lunghezza corrispondente di un tratto di parallelo è esprimibile mediante la seguente relazione trigonometrica:

Lunghezza del tratto di parallelo = lunghezza del corrispondente tratto di Equatore x coseno Latitudine

La lunghezza di un parallelo pertanto è sempre inferiore all'Equatore, mentre la sua proiezione, cadendo sul cilindro, risulta essere uguale all'Equatore. Si verifica cioè che un qualsiasi parallelo diventa, sulla proiezione, lungo quanto l'Equatore secondo la formula di deformazione:

Per semplicità e chiarezza prendiamo in esame solo una parte della superficie sferica e la relativa parte di proiezione cilindrica (Figura 9.3).

L'arco di parallelo ab, proiezione dell'arco di parallelo AB, risultando uguale all'arco di Equatore QQ', si è deformato dimensionalmente in funzione della secante della Latitudine di AB, ovvero:

Il meridiano Q'b, proiezione della Latitudine Q'B, giacendo sulla generatrice del cilindro tangente alla sfera, si è deformato dimensionalmente in funzione della tangente della Latitudine .

Poiché le deformazioni subite dai meridiani e dai paralleli non avvengono con la stessa funzione trigonometrica, la superficie proiettata non è isogona.

Immaginiamo ora di tagliare la superficie cilindrica lungo una generatrice e di svilupparla in piano:

Le circonferenze QLMN ed L'M'N' diventano linee rette parallele tra loro tutte uguali in lunghezza all'Equatore, il quale a sua volta rappresenta in lunghezza vera l'Equatore della sfera. La distanza tra un parallelo e l'altro è funzione della tangente della Latitudine dei paralleli stessi.

Le generatrici, proiezione dei meridiani, rimangono rette che invece di convergere ai poli con angoli uguali alla differenza di Longitudine, sono parallele tra loro (ovvero convergono all'infinito, come indicato anche dal valore di tang 90°).

Meridiani e paralleli sono quindi rappresentati da linee rette che s'intersecano a 90°. Intorno all'Equatore le deformazioni sono abbastanza contenute, ma aumentano con l'aumentare della Latitudine.

Visto che la proiezione non è isogona, e dato che per l'uso che vogliamo farne questa condizione è indispensabile, potremmo concludere dicendo che questo tipo di proiezione cilindrica non è idonea come Carta di Navigazione.Il cartografo olandese G. Kramer (Mercatore), per non modificare l'inquadratura generale della proiezione e nello stesso tempo pervenire all'isogonismo scoprì che era sufficiente far variare il parametro Latitudine in funzione della secante, ovvero nello stesso modo in cui avveniva la deformazione del parametro Longitudine. In tal modo, con un semplice spostamento dei paralleli, consistente nel distanziarli dall'Equatore in funzione della secante della loro Latitudine anziché della tangente, si ottenne di non variare la configurazione della proiezione che venne così resa isogona.

Si dimostra che le formule di corrispondenza della Carta di Mercatore sono:

Il procedimento matematico seguito da Mercatore parte dell'esame di due triangoli infinitesimi (ABC sulla sfera e abc sulla proiezione) i cui lati hanno i seguenti corrispondenti valori (Figura 9.4):

Affinché i due triangoli abbiano angoli corrispondenti uguali (requisito essenziale dell'isogonismo) è necessario che i lati stiano fra loro in proporzione:

ab : AB = bc : BC = ac : AC

Il valore del terzo rapporto è dato da:

Dl / Df cos f = sec f

Imponendo tale valore anche agli altri due rapporti si perviene all'isogonismo della Carta. In particolare, operando sul secondo rapporto si ha:

bc / BC = dy / df= secf

dy = df secf

e, integrando si ottiene:

y = loge tang (45° + f / 2)

nota come equazione della Latitudine crescente.

La stessa relazione può essere espressa in logaritmi decimali:

y = 7915,7 log tang (45° + f / 2)

Concludendo risulta chiaro che: per costruire matematicamente una Carta di Mercature sarà sufficiente far corrispondere sulla Carta alle coordinate f e l della sfera rappresentativa, le due coordinate X e Y ricavate dalle seguenti formule di corrispondenza:

dove:

2 p R l / 21.600                =          lunghezza di un primo di Equatore

l                                  =          Longitudine in primi

f                                  =          Latitudine in gradi

9.2       Impiego della Carta di Mercatore. Misura delle distanze.

Al fine di misurare correttamente la distanza ortodromica tra due punti, bisognerà ruotare intorno al suo punto centrale il tratto rettilineo di cui si vuol conoscere la distanza lossodromica, fino ad orientarlo per meridiano: la differenza di Latitudine fra gli estremi del segmento, espressa in primi, rappresenta in miglia la distanza cercata (Figura 9.5).

Se il segmento è molto lungo, conviene suddividerlo in più tratti, operando per ciascuno di essi come è stato sopra indicato, in quanto la scala della carta aumenta con la latitudine

Ogni foglio di una Carta di Mercatore porta una Scala: essa è rigorosamente valida per un solo parallelo, indicato generalmente sul foglio vicino al rapporto di riduzione.

9.3       Tracciamento delle Rotte e delle linee di posizione sulla Carta di Mercatore.

Il caratteristico reticolo ortogonale della Carta di Mercatore fa sì che una retta tracciata su di esso mantenga con i vari meridiani un angolo costante, ossia, come si suol dire, la Carta rettifica le lossodromie. È questa la sua caratteristica più apprezzabile.

Gli archi di cerchio massimo, invece, quando non siano archi di Equatore o di meridiano, sono rappresentati da curve che volgono la concavità sempre verso l'Equatore.

Abbiamo, in definitiva, che le Rotte lossodromiche possono essere tracciate agevolmente come linee rette, mentre invece, le Rotte ortodromiche non sono di facile tracciamento (Figura 9.6). Occorrerà infatti determinare una serie di coordinate di punti intermedi della Rotta ortodromica che si intende percorrere, riportarli sulla Carta di Mercatore e quindi tracciare le Rotte che congiungono i punti.

Si traccia in questo modo una spezzata che viene chiamata spezzata lossodromica, e che approssima la Rotta ortodromica con tanta migliore precisione quanto più piccola è la differenza di Longitudine tra i punti.

9.4       Tracciamento di Rilevamenti radioelettrici

Il tracciamento dei Rilevamenti radiogoniometrici (che si propagano secondo archi di circonferenza massima) avviene con metodi che variano secondo la distanza del velivolo dalla stazione. Più distante è il velivolo dalla stazione, tanto più distante risulta la lossodromia, tracciata in base allo stesso azimut, rispetto alla linea di posizione ortodromica (Figura 9.7).

Per la correttezza, più che di distanza conviene parlare di differenza di Longitudine tra il velivolo e la stazione, perché è proprio da questa differenza che dipende lo scostamento dell'ortodromia dalla lossodromia tra gli stessi punti.

Per valori di differenza di Longitudine inferiori a 2° la lossodromia e l'ortodromia si possono ritenere coincidenti e pertanto basta tracciare, in prossimità della posizione stimata del velivolo un segmento orientato secondo il valore del Rilevamento comunicato da Terra o del Radiale VOR (Figura 9.8).

Per valori di differenza di Longitudine compresi tra i 2° ed i 6°, lo scostamento diventa sensibile, ma non così forte da non poter accettare, come linea di posizione un tratto di lossodromia di azimut leggermente diverso da quello dell'ortodromia.

La differenza fra i due azimut, come si vede nella Figura 9.9, è rappresentato dall'angolo γ.

L'angolo γ va sotto il nome di correzione di Givry, ed è dato dalla seguente formula:

Dove:

Δl = differenza di Longitudine tra la posizione della stazione a Terra e la posizione dell'aereo;

Φmed = Latitudine media tra la posizione della stazione a Terra e la posizione dell'aereo.

Per valori di differenza di Longitudine maggiori di 6°, non basta più correggere l'azimut dell'angolo γ perché le due linee in prossimità della posizione stimata assumono direzioni alquanto diverse.

In quest'ultimo caso, la questione si risolve praticamente tracciando, nel punto in cui la lossodromia di azimut QTE + γ incontra il meridiano stimato, un segmento di retta, inclinato rispetto al Rilevamento lossodromico (QTE + γ) dell'angolo γ (Figura 9.10). In questo modo, la linea così tracciata approssima in modo migliore l'andamento reale del luogo di posizione nel punto considerato.

•  Per γ < 2° non si apportano correzioni
•  Per γ compreso tra 2° e 6° si apporta la correzione semplicemente
•  Per γ > 6° si apporta la correzione, ed all'incontro del QTE + γ col meridiano stimato si traccia il segmento inclinato di γ rispetto al QTE + γ.

Per quanto riguarda il segno della correzione, è facile ricordare la seguente regola pratica: la correzione di Givry si applica sempre in modo da portare la direzione del Rilevamento verso l'Equatore.

9.5       Tracciamento di archi di cerchio minore

Sulla Carta di Mercatore gli archi di cerchio minore sono rappresentati da curve di difficile tracciamento, e il loro andamento può variare in funzione della posizione relativa del cerchio minore rispetto ai poli (Figura 9.11).

9.6       Tracciamento di Rilevamenti radiogoniometrici presi da bordo

Il luogo di posizione considerato è del tutto dissimile rispetto al luogo di posizione che deriva dal Rilevamento preso da Terra.

Il Rilevamento radiogoniometrico preso da bordo è un Rilevamento polare, riferito cioè, all'asse longitudinale del velivolo. Per ottenere il Rilevamento vero basta sommare al Rilevamento polare la Prua vera.

La linea di posizione che ne deriva è un arco di cerchio minore che più propriamente prende il nome di linea isoazimutale, perché si tratta di una linea lungo la quale l'azimut della stazione rispetto al velivolo rimane costante.

È interessante conoscere l'andamento di questa linea, non perché occorra effettuarne il preciso tracciamento, ma al fine di avere un'idea chiara della corrispondenza, senso ed grado di approssimazione della retta cui necessariamente occorrerà riferirsi se si vorrà risolvere il problema sulla Carta.

Per comprendere bene il significato e l'andamento della linea isoazimutale si può ragionare nel seguente modo: se un aereo rileva simultaneamente due stazioni rispetto al Nord, ottiene due azimut la cui differenza definisce un luogo di posizione rappresentato da un cerchio passante per le due stazioni e per il punto in cui si trova l'aereo nell'istante a cui si riferisce la misura effettuata da bordo (Figura 9.12).

La linea prende il nome di curva di uguale differenza di azimut.

Supponiamo ora che i due radiofari si trovino nell'emisfero Nord; se immaginiamo di situarne uno al polo, il suo Azimut risulterà sempre uguale a zero. In questo modo la differenza degli Azimut sarà data dalla misura relativa ad una sola stazione; ne risulterà che la curva avrà ancora lo stesso andamento; passerà cioè per l'aeromobile, per la stazione e per il polo, ma resterà definita da un solo azimut (Figura 9.13).

La isoazimutale è quindi il luogo geometrico dei punti della superficie terrestre dai quali una stazione viene rilevata sempre sotto lo stesso angolo; questa è una linea corrispondente ad un arco di cerchio passante per il polo, per l'aereo e per la stazione di Terra.

Normalmente, per brevi distanze, la linea può essere tracciata sulla carta di Mercatore senza commettere un errore apprezzabile mediante una linea retta.

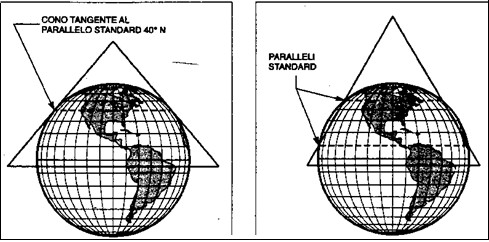
9.7       Carta di Lambert.

La Carta di Lambert è una proiezione modificata derivata da una proiezione conica generalmente secante.

La proiezione conica retta si ottiene proiettando la superficie da rappresentare, su un cono che può essere tangente o secante alla sfera rappresentativa, ed il cui asse coincide con quello terrestre.

La lunghezza del parallelo di tangenza o dei due di secanza è riprodotta sulla proiezione in grandezza vera, e sarà questa (o queste) la linea isomecoica della proiezione. Secondo quanto già detto, solo su questa linea è rigorosamente valida la Scala della Carta (Figura 9.14).

Congiungendo il centro della sfera rappresentativa con un parallelo di Latitudine Φ, si ottiene un cono di proiezione coassiale con il cono del quadro; la loro intersezione sarà una circonferenza (il cui centro giace sull'asse comune dei due coni) e rappresenterà la proiezione di quel parallelo sulla superficie del quadro.

Sviluppando il cono di proiezione su un piano, i paralleli saranno rappresentati da archi di cerchio aventi il centro nel polo.

La proiezione dei meridiani dal centro della Terra sul cono sarà rappresentata da rette convergenti nel polo, e passanti per il corrispondente meridiano nel punto di tangenza o nei punti di secanza del cono con la superficie sferica.

Sulla Carta sviluppata i meridiani saranno quindi rettilinei e convergenti verso il polo (Figura 9.15).

Si consideri per il momento una proiezione conica tangente.

Quando il cono viene sviluppato su di un piano, si ottiene una figura simile a quella della Figura 9.16.

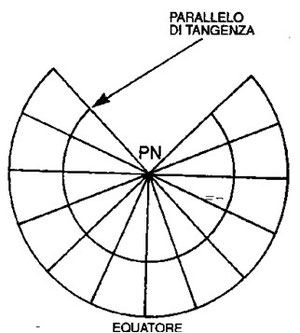
I paralleli si sviluppano secondo archi di circonferenza tutti concentrici al polo.

Il parallelo di tangenza, che è lungo esattamente quanto quello della sfera rappresentativa, si sviluppa su un arco di cerchio il cui raggio è dato dalla relazione:

r = R cotg Φt

dove, come si vede dalle Figure 9.17 e 9.18:

r           =          raggio del cerchio che raffigura il parallelo di tangenza

R         =          raggio della sfera rappresentativa

Φt        =          Latitudine di tangenza

La lunghezza del parallelo di tangenza è data dalla seguente relazione:

lunghezza del parallelo di tangenza = 2 π R cos Φt

L'angolo C° fra due meridiani rappresenta la proiezione della differenza di Longitudine Δλ° ed è chiamato Angolo di convergenza.

L'angolo di convergenza ° sulla proiezione, è uguale alla differenza di Longitudine ° sulla sfera moltiplicata per il seno della Latitudine di tangenza t.

γ° = Δλ sen Φt 

La dimostrazione della relazione sopra riportata è la seguente:

α = (2 π R cos Φt) / (R cotg Φt)

semplificando:

α = (2 π cos Φt) / cotg Φt

cotg Φt = α = cos Φt / sen Φt

quindi:

α = (2 π cos Φt) / (cos Φt / sen Φt)

semplificando:

α = 2 π sen Φt

Per determinare sulla sfera l'angolo di convergenza C° compreso fra due meridiani di differenza di Longitudine Δλ nota, basterà impostare la proporzione:

(2 π sen Φt) / (2 π) = C° / Δλ

da cui:

C° = Δλ sen Φt

Il termine "sen Φt" è chiamato "costante di convergenza" e normalmente viene indicato con la lettera K. Esso è un parametro caratteristico di ogni proiezione conica.

La proiezione cilindrica retta non è isogona. Il cartografo francese Lambert la rese isogona con procedimento analogo a quello seguito dal Mercatore. Le formule di corrispondenza della Carta di Lambert sono:

γ = K Δλ

ρ = tang (45° - Φt / 2)K

Molto frequentemente la Carta di Lambert viene realizzata utilizzando per la costruzione un cono secante la sfera in due paralleli chiamati standard (Figura 9.19).

Le proprietà della Carta sono le stesse di quelle esaminate precedentemente, e sono applicabili le stesse relazioni matematiche, con l'avvertenza di utilizzare la Latitudine media dei due paralleli standard al posto della Latitudine di tangenza.

Il motivo che induce all'utilizzazione di un cono secante invece di uno tangente è quello di minimizzare le deformazioni; quello di avere in definitiva una Carta in grado di rappresentare la superficie terrestre nel modo migliore per una fascia di latitudini più ampia possibile.

9.8       Impiego della Carta di Lambert. Misura delle distanze.

Un segmento rettilineo rappresenta sulla Carta di Lambert con grande approssimazione, un percorso ortodromico. La Carta è isogona ed i meridiani sono rettilinei: è quindi agevole determinare gli angoli con cui l'ortodromia taglia i vari meridiani.

Se il tratto da percorrere è breve, e comunque fino a quando la differenza fra l'angolo di Rotta iniziale e quello finale non supera i 3° circa, il tratto rettilineo fra i due punti si può ritenere coincidente con il corrispondente arco di lossodromia; si assume allora come angolo di Rotta vera quello riferito al meridiano corrispondente alla Longitudine media tra i due punti (Figura 9.20).

Se la differenza di Longitudine fra i due meridiani è piuttosto alta od anche se la convergenza sulla Carta è piuttosto forte (ciò si verifica per percorsi anche non molto lunghi alle alte latitudini) bisogna dividere il percorso in tanti tratti, fino a riportarsi, per ogni segmento, nelle condizioni sopra indicate.

Se ad esempio sul percorso Gander - Reykjavik, dove la Rotta iniziale è 036° e quella finale 064°, si volesse percorrere l'intero tratto utilizzando la Rotta media:

(036° + 064°) / 2 = 050°

si percorrerebbe una lossodromia molto scostata dal percorso ortodromico (Figura 9.21); ciò comporterebbe un notevole allungamento del percorso. Inoltre non si avrebbe la possibilità di tracciare speditamente la Rotta sulla Carta. Occorre quindi spezzare la Rotta in numerosi tratti, in modo da riportarsi nelle condizioni sopra esposte, e quindi calcolare la Rotta media per ogni segmento.

9.10    Proiezione stereografica della zona polare.

Si ottiene proiettando la calotta polare su di un piano perpendicolare all'asse dei Poli e prendendo come punto di vista il Polo opposto a quello della zona che si vuol rappresentare (Figura 9.22).

Il piano di proiezione può essere tangente o secante alla sfera.

Per le nostre rappresentazioni useremo il piano secante all'Equatore.

La proiezione dei meridiani sul piano equatoriale secante è costituita da linee rette convergenti verso un punto coincidente con il centro della Terra, e rappresentativo del polo.

L'angolo formato dalla proiezione di due meridiani è l'angolo di convergenza °. Nel caso particolare, questo sottende un arco di Equatore uguale alla differenza di Longitudine.

L'angolo di convergenza quindi risulterà uguale alla differenza di Longitudine.

γ° = Δλ

Proiettando un parallelo dal polo opposto, si ottiene un cono di proiezione il cui asse coincide con l'asse di proiezione:

L'intersezione del cono con il piano di proiezione è una circonferenza il cui centro coincide con la proiezione del polo ed il cui raggio andiamo a determinare.

Immaginiamo di dover proiettare il parallelo Φo la cui colatitudine è rappresentata dall'arco PT. La proiezione di detto arco è il raggio ρ della circonferenza che rappresenta la proiezione di quel parallelo.

Nel triangolo OTP' l'angolo esterno POT rappresenta la colatitudine di Φo.

L'angolo in P' essendo metà di quello al centro rappresenterà la semicolatitudine e sarà:

P' = (90 - Φo) / 2 = 45 - (Φo / 2)

Ne consegue che nel triangolo P'OL il lato OL = ρ sarà dato da:

ρ = R tang [45 - (Φo / 2)]

Questa è la formula di corrispondenza per la Latitudine, da cui discende che la proiezione è naturalmente isogona.

9.11    Impiego della Carta stereografica polare. Misura di angoli e distanze.

L'impiego della Carta stereografica polare è limitata strettamente alle tratte che prevedono il sorvolo di zone vicine ai poli. Se si opera a latitudini inferiori, è più conveniente l'uso di Carte realizzate con proiezione di Lambert.

Poiché la proiezione è naturalmente isogona ed i meridiani sono rappresentati da linee rette, la misura di un angolo è altrettanto facile quanto sulle Carte di Mercatore e di Lambert.

Una linea retta indica, con la stessa approssimazione della Carta di Lambert, l'arco di ortodromia che passa per due punti sulla sfera terrestre.

Operando a elevate latitudini, onde poter mantenere a pochi gradi la variazione dell'angolo di Rotta da un estremo all'altro di ciascuna tratta, occorrerebbe suddividere l'intero percorso in moltissimi brevi segmenti. L'operazione sarebbe inoltre notevolmente complicata per la frequente variazione della declinazione magnetica, per non parlare poi dell'inattendibilità della bussola magnetica in aree prossime ai poli magnetici. A volte il procedimento può riuscire tanto complicato e soggetto ad errori da rendere del tutto inefficaci, in quelle regioni, i comuni metodi della Navigazione stimata; si ricorre quindi a tecniche particolari, quale la Navigazione Griglia o quella condotta con sistemi di Navigazione Inerziale o GPS.

La Scala delle distanze, non è costante. Essa varia (cresce) con l'aumentare della distanza del punto considerato dal Polo. Però anche in questo caso, così come nella Carta di Lambert, il modulo di deformazione non è elevato, quindi nel valutare una distanza non e indispensabile misurare sulla Latitudine media con precisione; eventuali lievi spostamenti delle misure lungo il meridiano non comportano gravi errori.

9.12    Proiezione gnomonica

Per la risoluzione di alcuni particolari problemi della Navigazione sono molto utili le proiezioni gnomoniche, che sono proiezioni prospettiche centrografiche tangenti (Figura 9.23).

Tali proiezioni godono della proprietà di rappresentare con linee rette i circoli massimi.

È precisamente questa proprietà che le rende utilmente impiegabili nella risoluzione dei problemi della Navigazione ortodromica.

Si distinguono proiezioni gnomoniche di tre tipi, a seconda della posizione che occupa il punto di tangenza sulla sfera rappresentativa:

           proiezione gnomonica equatoriale, se il punto di tangenza è un punto dell'Equatore;

           proiezione gnomonica polare, se il punto di tangenza occupa uno dei poli;

           proiezione gnomonica orizzontale o meridiana se il punto di tangenza è situato ad una qualsiasi Latitudine.

La gnomonica equatoriale (Carta di Hilleret) è usata per la determinazione delle Rotte ortodromiche su lunghi percorsi. Tali Rotte vengono poi trasportate per punti sulle Carte di Lambert e divise in tratte di 200 - 300 miglia, lungo le quali si effettua normalmente la Navigazione lossodromica.

La Carta gnomonica non è isogona, non è equidistante, non è equivalente. L'unica caratteristica positiva importante è che le ortodromie sono rappresentate come linee rette.

Dovendo quindi pianificare una Rotta tra aeroporti molto lontani, è possibile utilizzarla proficuamente per determinare il percorso più breve.

Su questa Carta è però difficile ricavare i valori di angolo di Rotta, in quanto meridiani e paralleli non si intersecano ad angolo retto, ed anche la determinazione delle distanze è difficile a causa della variabilità della Scala (Figura 9.24).

L'unico uso che se ne può fare è quindi quello di determinare una serie di Waypoints intermedi, spezzando la Rotta in un certo numero di segmenti, e quindi di riportarli su una Carta isogona quale quella di Mercatore o di Lambert, sulla quale tracciare nuovamente la Rotta, punto per punto. Diventa così agevole la misura degli angoli di Rotta e delle distanze.

9.13    Carte aeronautiche di corrente uso.

Le Carte ritenute necessarie per la moderna Navigazione aerea, a vista o strumentale, sono descritte dall'ICAO nell'Annesso 4, "Aeronautical Charts", unitamente agli standards e alle raccomandazioni da adottare per la loro costruzione ed interpretazione (vedi Parte 1 regolamentazione aeronautica); se ne riporta un elenco.

           Carte degli ostacoli aeroportuali: hanno la funzione di mettere in evidenza gli ostacoli presenti nell'area aeroportuale, le quote minime e le procedure atte ad evitarli.

           Carte per la pianificazione: le "plotting charts" servono ai piloti per la pianificazione di lunghi voli, specialmente in zone oceaniche, e per annotare durante l'effettuazione del volo le successive posizioni dell'aereo e verificare la correttezza della Navigazione.

           Carte di Radionavigazione (RFC o Radio Facility Chart): servono per facilitare l'utilizzo dei radioaiuti alla Navigazione, evidenziare le Rotte ATS e le informazioni che le riguardano. Possono essere divise in "H" o "L", a seconda che riguardino lo spazio aereo superiore o inferiore, per quelle zone in cui ci siano molte informazioni da riportare; vi sono anche Carte dedicate unicamente alle Rotte RNAV.

           Carte delle aree terminali: per le aree dove è istituita una TMA, riportano tutte le informazioni necessarie per la transizione dalla fase di volo in Rotta a quella di avvicinamento finale, e dal decollo alla fase di volo in Rotta.

           Carte di avvicinamento strumentale (IAL); forniscono la rappresentazione grafica delle traiettorie di avvicinamento strumentale, di mancato avvicinamento e di attesa relative all'aeroporto considerato (Scala raccomandata 1:350.000).

           Carte aeronautiche del mondo 1:1.000.000: usate per la pianificazione e l'effettuazione della Navigazione a vista. Sono realizzate in proiezione di Lambert per le latitudini fino ad 80°, e con proiezione stereografica polare fra gli 80° e i poli.

           Carte aeronautiche 1:500.000: usate per la Navigazione a vista a breve e medio raggio condotta a bassa velocità e bassa quota.

           Carte di avvicinamento a vista: sono particolarmente necessarie per gli aeroporti sprovvisti di Radioassistenze; riportano le traiettorie di avvicinamento da seguire con riferimento al terreno, in Scala 1:200.000 o 1:250.000.

           Carte di atterraggio: forniscono le informazioni necessarie all'avvicinamento alla pista di atterraggio e allo sgombero della pista;

           Carte aeroportuali: usate per il movimento al suolo degli aeromobili tra le piste ed i piazzali, e per mostrare l'ubicazione delle principali attrezzature di assistenza al volo esistenti negli aeroporti di grandi dimensioni;

           Carte di Navigazione aerea in Scala piccola: forniscono agli aeromobili che operano ad alta quota ed alta velocità il mezzo per riconoscere punti caratteristici esistenti su aree molto estese, sulle regioni mancanti di radioaiuti o sulle quali la Navigazione a vista si rende preferibile o necessaria.

           Carte del terreno per gli avvicinamenti di precisione: rappresentano nei dettagli la planimetria degli ultimi 900 metri dell'avvicinamento, necessaria per stabilire gli effetti del terreno nella determinazione dell'altezza radioaltimetrica per tutte le piste servite da avvicinamenti di precisione di Categoria II e III.

In appendice all'Annesso 4, l'ICAO riporta le tavole dei simboli con cui devono essere rappresentati gli elementi topografici e idrografici quali i rilievi, i fiumi, i laghi e le coste; le opere dell'uomo come le città, le strade, le ferrovie, gli ostacoli artificiali, i confini politici, gli elementi aeronautici come gli aeroporti, le Radioassistenze, le Rotte ATS e i confini dei vari spazi aerei. Questi simboli vengono riprodotti nelle legende delle Carte, direttamente in calce ad esse o, in un'apposita sezione del "Route Manual".

Nelle Carte di Navigazione a vista, ed in quelle strumentali il cui uso è necessario quando si opera vicino ad ostacoli è particolarmente importante che i rilievi siano rappresentati chiaramente. Su queste Carte sono segnalate le "spot elevations", quote di ostacoli naturali e artificiali significativi, in piedi o in metri (l'unità di misura è riportata nella legenda). Queste indicazioni, pur fornendo un'idea degli ostacoli più alti, da sole non permettono di avere una visione di tutto il sistema orografico della zona. Per questo su molte Carte viene adattato il sistema delle "linee ipsometriche" o "Isoipse", abbinato alla tinteggiatura ipsometrica.

Le linee ipsometriche sono linee immaginarie che uniscono tutti i punti situati alla stessa elevazione sul livello del mare. Esse vengono rappresentate sulla Carta ad intervalli regolari (per esempio ogni 500 piedi), permettendo di individuare l'elevazione di qualsiasi punto intermedio per interpolazione fra due Isoipse, e di apprezzare la pendenza del terreno valutando la vicinanza delle linee ipsometriche.

La tinteggiatura viene abbinata per rendere ancora più evidente la morfologia del terreno. Con strati di tinte ipsometriche, zone di elevazioni successive sono colorate differentemente. Per convenzione, i colori usati seguono lo spettro, cominciando con il verde per le quote più basse, e procedendo attraverso diverse gradazioni di beige e di arancione fino al rosso scuro e al viola per quelle più alte. Le Carte di area terminale e le IAL del gruppo ATLAS riportano al massimo cinque strati, corrispondenti a quattro curve di livello, e partendo dall'elevazione dell'aeroporto rappresentano in bianco la zona con elevazione compresa entro i primi 500 piedi, e con quattro gradazioni di ocra via via più scure rappresentano le elevazioni fino a 1.500, 2.500, 3.500, ed oltre 3.500 piedi dalla elevazione dell'aeroporto.

Nelle IAL vengono riportati anche tutti quegli ostacoli che sporgono da un immaginario piano inclinato di 100 ft/miglio entro 5 miglia dall'aeroporto, o entro le aree di avvicinamento e mancato avvicinamento.

Su tutte le Carte aeronautiche viene indicato, il valore numerico della Scala utilizzata per la rappresentazione. Essa è rigorosamente vera lungo le linee isomecoiche, che corrispondono ai paralleli di tangenza o di secanza delle proiezioni per sviluppo. Questi paralleli sono indicati sulla Carta vicino al tipo di proiezione e al rapporto di riduzione. Per tutti gli altri punti la Scala risulta distorta secondo il modulo di deformazione lineare della Carta.

La Scala grafica viene invece riportata solo sulle Carte che non hanno rappresentazione del reticolato geografico, come ad esempio le Carte aeroportuali. Per tutte le altre Carte la presenza di una graduazione in primi di Latitudine rende superflua la riproduzione della Scala grafica.